En variedad de situaciones se requiere tomar decisiones a partir de la comparación de valores, por ejemplo encender un ventilador cuando la temperatura ambiente sea mayor a 26 °C, apagar la luz cuando el nivel de luz solar sea mayor a un umbral, decidir si un robot da vuelta a la izquierda o derecha dependiendo la medición de un sensor de distancia, entre otras muchas aplicaciones. Este tipo de circuitos comparadores puede decirnos si dos números son iguales, o cuál de los dos es el mayor y menor.
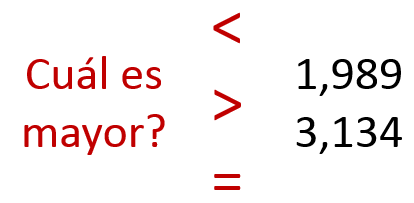
En este caso, normalmente ya estamos acostumbrados a comparar este tipo de valores, sin pensar mucho podemos ver que el 3,134 es mayor que el 1,989. Pero, cómo realizamos la comparación? si comparamos uno a uno cada dígito, podemos ver que la mayoría de los dígitos del primer número (1,989) son mayores que los valores en cada dígitos del número de abajo, pero aún así el 3,134 es mayor, cómo lo decidimos? Dependiendo la posición de cada dígito representa valores diferentes, en este caso al ser números decimales, cada posición representa una potencia de 10: 103 102 101 100, lo que es igual a 1000 100 10 1, por lo que cada dígito representa 1000 900 80 9 = 1989 en este ejemplo. Para decidir entonces cuál número es mayor, se comienza a comparar por los dígitos más significativos (los de la izquierda), el número que tenga un valor mayor en sus dígitos más a la izquierda será el número mayor, sin importar el resto:
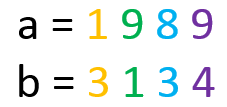
En este caso, desde el primer dígito de la izquierda (color anaranjado) se puede decidir que el 3 es mayor que el 1, por lo tanto “b” es mayor que “a” sin importar el resto de los dígitos. En otro ejemplo:

Aquí el procedimiento para realizar la comparación es igual, pero podemos ver que los dígitos más significativos (los de más a la izquierda) son iguales, por lo que se deben seguir comparando los restantes:

En este otro ejemplo, la decisión sobre cuál número es mayor se toma hasta el tercer dígito, dado que los primeros 2 son iguales, entonces se ve que el 8 es mayor que 7 y por lo tanto el número “a” es mayor que “b”.
Circuito comparador de magnitudes de 4 bits (74LS85)
Existen diferentes circuitos comparadores, algunos analógicos, otros digitales, con diferentes características y capacidades. En esta ocasión hablaremos del 74LS85, un comparador de magnitudes digital, con capacidad de 4 bits, esto quiere decir que podemos comparar 2 números de hasta 4 dígitos binarios y resolver cuál de los dos es mayor, menor o si son iguales. Este circuito tiene 16 terminales:
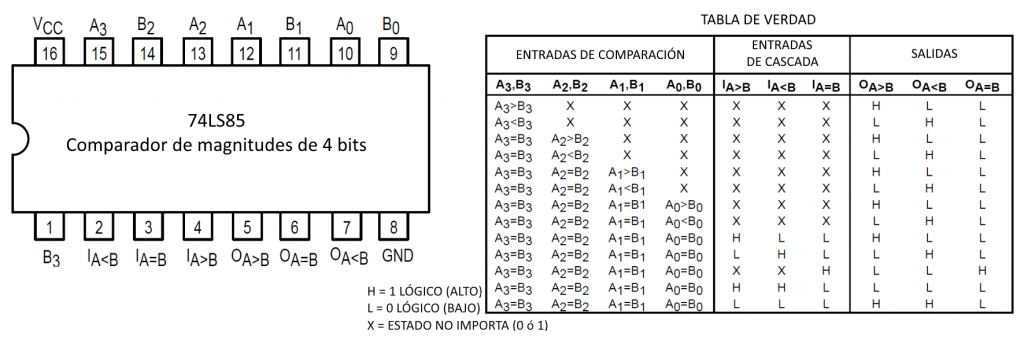
El 74LS85 cuenta con 2 entradas de 4 bits cada una, 3 salidas para representar si un valor es mayor, menor o igual al otro, sus entradas de alimentación (Vcc y Gnd) además de 3 entradas más llamadas entradas de cascada que tienen como objetivo enlazar 2 o más circuitos 74LS85 para ampliar la capacidad del comparador de magnitudes y así convertirlo en un comparador de 8 bits, 12 bits o más, dependiendo del número de circuitos que se acoplen.
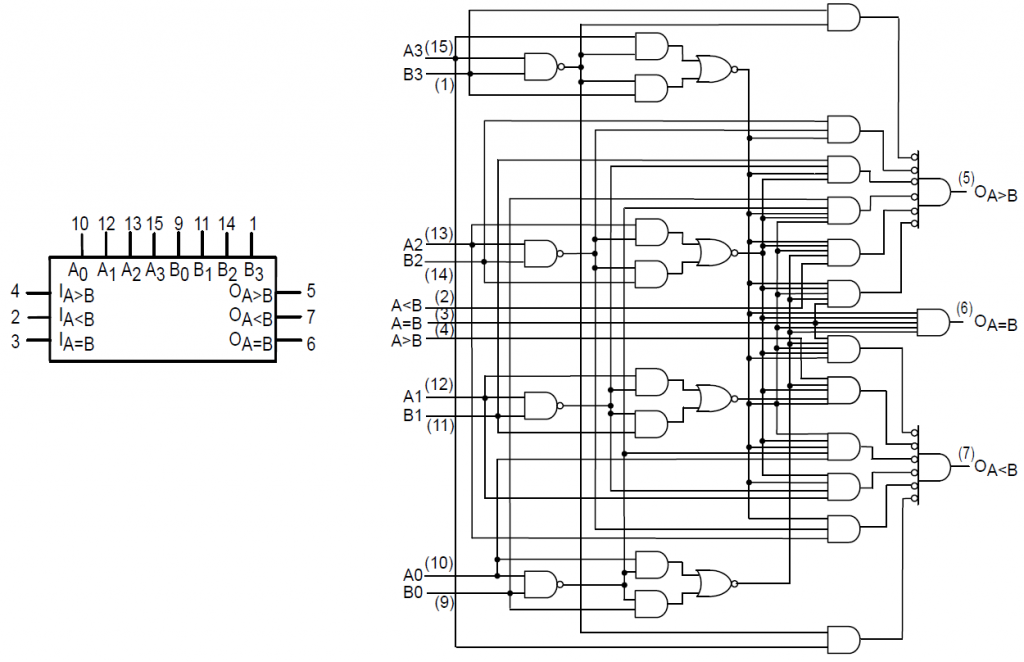
En la tabla de verdad se aprecia que la comparación entrega el resultado a través de sus 3 salidas OA>B, OA<B y OA=B, solo una de ellas debe tener un valor en ALTO (H) y las otras dos en BAJO (L), si no se cumple esto es que se tiene una entrada no válida. El resultado se decide del mismo modo que se describió anteriormente, comparando dígito a dígito comenzando con el dígito más significativo (el de la izquierda) en este caso, si suponemos 2 entradas A y B de 4 bits cada una, quedarían acomodadas de esta forma:
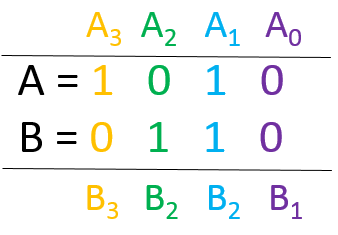
A los bit más significativos se le llamará A3 y B3, primero se comparan entre ellos dos, si la decisión se puede tomar desde este punto, entonces ya no imparta el valor de los otros dígitos, como en este ejemplo, se puede ver que A3 > B3, por lo tanto se decide que A > B, entonces las salidas serían OA>B=H, OA<B=L y OA=B=L. Si A3 = B3, entonces se comparan A2 y B2, y así sucesivamente hasta llegar a A0 y B0. Si vemos la tabla de verdad, las entradas de cascada solo se consideran cuando los 4 bits de A son iguales a los 4 bits de B y existe un único caso en la tabla de verdad donde el resultado final es A = B.

La decisión entonces si A o B es mayor se toma comparando bit a bit, si los 4 bits son iguales, entonces la decisión está dada por las entradas de cascada. La idea de las entradas de cascada es conectarse “en cascada” con otros circuitos 74LS85 iguales y su funcionamiento se puede reducir a que el valor de las entradas de cascada se “transfiere” a las salidas directamente cuando A = B. En esta tabla de verdad se ilustran los diferentes casos, si las entradas de cascada dicen que IA>B=H entonces esa será la salida OA>B=H (caso anaranjado), si IA<B=H entonces esa será la salida OA<B=H (caso azul) y si la entrada IA=B=H entonces esa será la salida OA=B=H (caso verde). Los casos en color rojo no son válidos, dado que en las entradas de cascada no debe de existir más de una entrada en ALTO (H) ni tampoco puede ser que todas las entradas sean BAJO (L). En resumen, las entradas de cascada están diseñadas para conectar varios circuitos, si solo se desea utilizar un solo circuito comparador entonces se deben conectar como sigue:
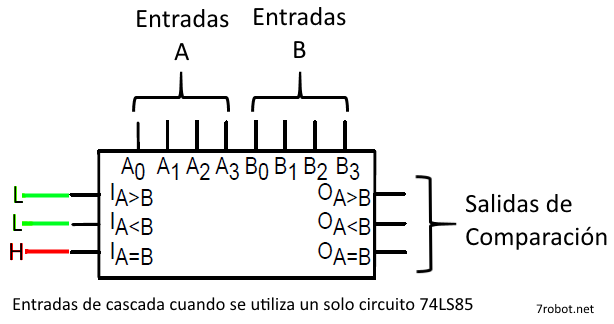
Si se desea ampliar la capacidad del comparador entonces se debe conectar de esta forma:
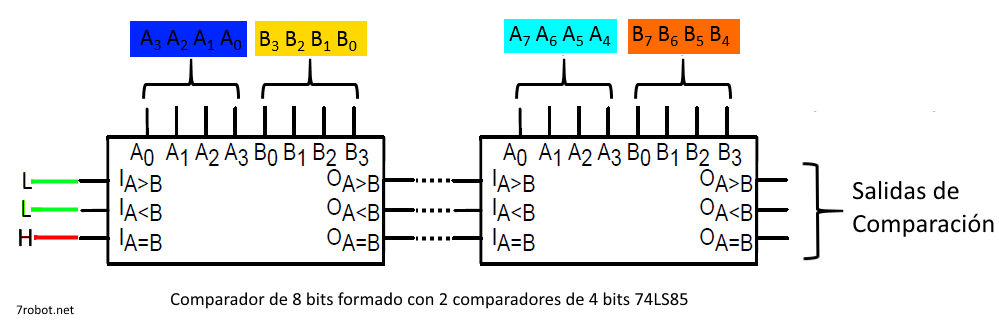
Como se comentó anteriormente, los bits más significativos son los que deciden el resultado de la comparación, y si son iguales los 4 bits entonces se revisan las entradas de cascada para tomar la decisión, en este caso, si comparamos dos número de 8 bits, el resultado de si A es mayor o no que B se decide con los primeros 4 bits (A7-A4), si estos 4 bits son iguales, entonces no se puede decidir si uno es mayor o no y tiene que considerar los 4 bits menos significativos restantes (A3-A0) para tomar la decisión. Si estos últimos 4 bits también llegaran a ser iguales, entonces se consideran las entradas de cascada del segundo circuitos (el de la izquierda) que en este caso arrojaría A=B por la conexión que se realiza.

Ejercicio comparador de magnitudes
Una práctica que utilice un comparador de magnitudes de 4 bits y además incorpore algunos de los circuitos MSI vistos en los temas anteriores puede ayudar a mejorar la comprensión de los temas, se proponen los siguientes requerimientos:
Dos entradas de 4 bits (4 bits en A y 4 bits en B)
Un único display de 7 segmentos será la salida
Se deberá mostrar en el display de 7 segmentos el número mayor entre A y B
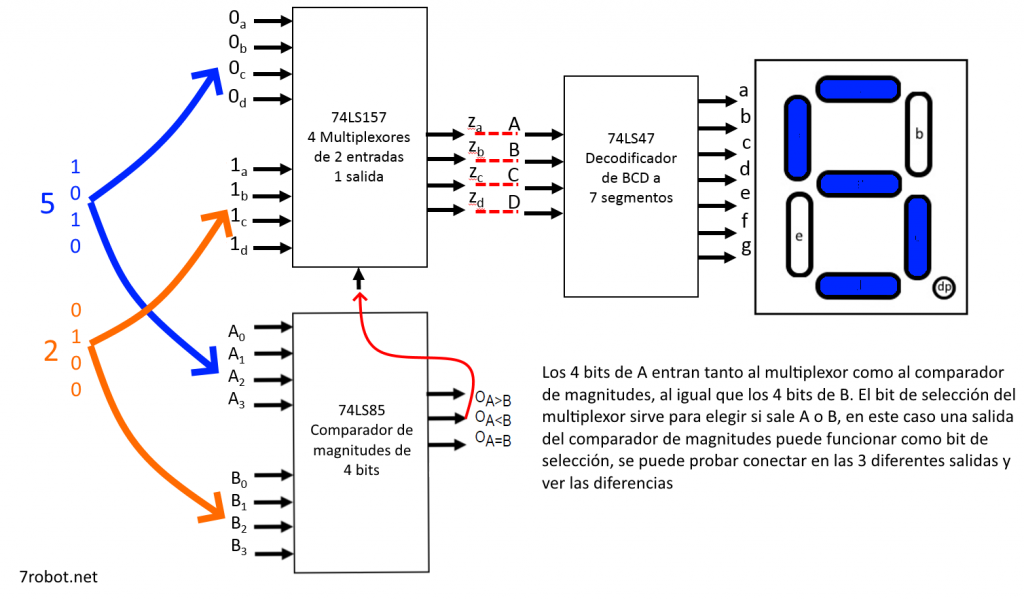
Por ejemplo, si se tienen A = 5 y B = 2, el display debe mostrar un 5. Si B cambia a 7 y A se mantiene en 5, entonces se debe mostrar un 7 en el display automáticamente:
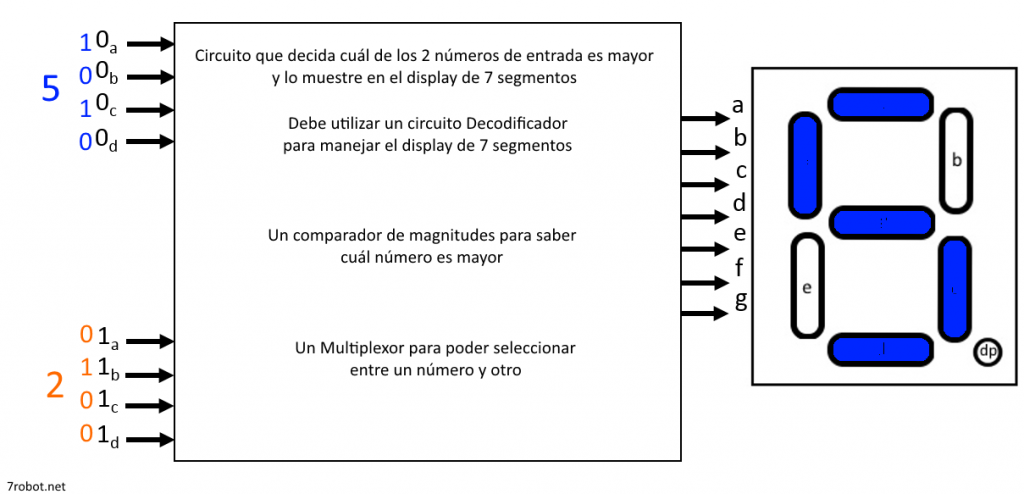
Parte de este circuitos se resolvió en el tema anterior, Multiplexores. Si se implementa, faltaría ver el modo de incorporarle el comparador de magnitudes para que la decisión de cuál de las dos entradas elegir sea de forma automática, dado que en la práctica anterior se debe elegir manualmente si mostrar uno u otro.
Simulación del comparador de magnitudes
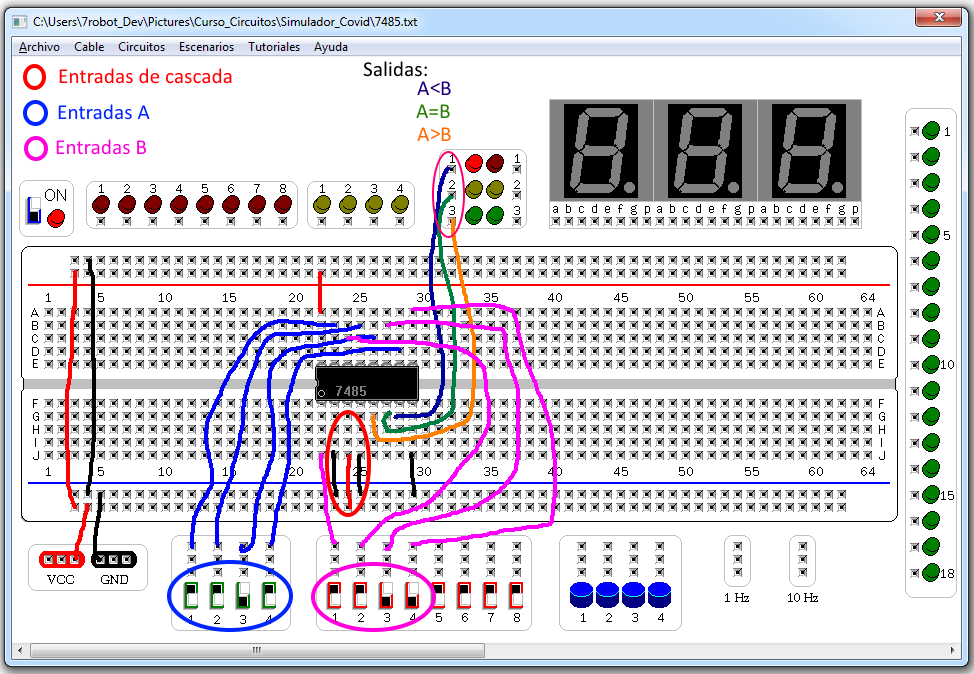
Un ejemplo de conexión de un solo circuito comparador de magnitudes con sus 2 entradas de 4 bits conectadas a interruptores y sus 3 salidas a LED’s se muestra a continuación. Al ser un solo circuito comparador de magnitudes, sus entradas de cascada quedan fijas con la entrada IA=B en ALTO como se recomienda.
Los 4 bits de entrada en A se conectaron con cables azules, los 4 bits de B con cables rosa, las entradas de cascada están señaladas en un ovalo rojo y las salidas se muestran arriba. Este archivo de simulación está disponible para su descarga aquí. Para obtener el simulador y ver cómo funciona, en el siguiente enlace:

Simulador de circuitos digitales
Existen diferentes simuladores de circuitos digitales disponibles para practicar y probar conexiones de circuitos lógicos, compuertas lógicas y una gran variedad de componentes. En particular aquí mostraremos el uso de un simuladorLeer más…
La idea de solución a la práctica propuesta está aquí por si deseas consultar.
| Sistemas MSI | Tema anterior | Tema siguiente |

Aplicaciones con sistemas MSIEscala de Integración A simple vista, resultaría difícil poder reconocer el funcionamiento de un circuito integrado, podemos ver el número de pines (terminales) que tiene, su tamaño o tipo de circuito integradoLeer más… |
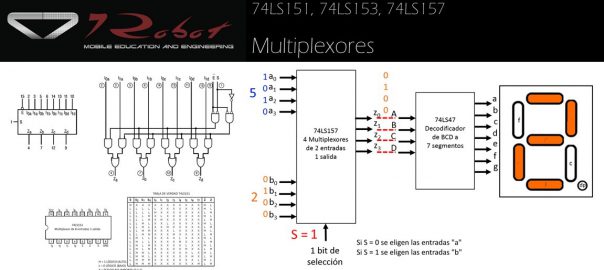
MultiplexoresEn general podemos encontrar multiplexores en diferentes ámbitos, como en equipo de audio, video, cómputo, así como en los sistemas digitales. Para mostrar la idea de su función veamos un ejemplo, laLeer más… | Sumadores (Pendiente) |
(7478)